COMPETENCIA 5

Contenido

Introducción.

1 ECUACIONES DIFERENCIALES ORDINARIAS
2 Método de Euler
3 Método de Taylor
4 Métodos de Runge-Kutta

5 Conclusión

6 Bibliográfia. 

INTRODUCCION.

Muchos problemas básicos de las ciencias experimentales pueden ser modelados usando ecuaciones ´ donde aparecen involucradas una función junto con sus derivadas. En este caso nos centraremos en el estudio de este tipo de ecuaciones y veremos como pueden ser resueltas utilizando lo ya estudiado en los temas anteriores. Comenzaremos definiendo lo que entenderemos por ecuación diferencial ordinaria y dando varios ejemplos clásicos de su uso en las ciencias experimentales.

El objetivo de este tema es exponer muy breve mente algunos de los conceptos básicos relacionados con las ecuaciones diferenciales ordinarias, con el objetivo de mostrar las técnicas elementales de su resolución numérica. Queda fuera del objetivo de estas notas, el estudio analítico de los problemas considerados. Una ecuación diferencial es una ecuación en que la incógnita es una función: no el valor de la función en uno o varios puntos, sino la función en si misma. Ademas, la ecuación involucra no solo la función (incógnita), sino también sus derivadas hasta un cierto orden. Cuando la incógnita es una función de una sola variable se dice que la ecuación es ordinaria, debido a que la o las derivadas que aparecen son derivadas ordinarias (por contraposición a las derivadas parciales de las funciones de varias variables)

ECUACIONES DIFERENCIALES ORDINARIAS 

En matemáticas, una ecuación diferencial ordinaria (comúnmente abreviada "EDO") es la ecuación diferencial que relaciona una función desconocida de una variable independiente con sus derivadas. Es decir, una sola variable independiente (a diferencia de las ecuaciones diferenciales parciales que involucran derivadas parciales de varias variables), y una o más de sus derivadas respecto de tal variable.

En ingeniería, ciencias naturales y sociales hay muchos problemas de interés que, cuando se plantean, exigen la determinación de una función la cual debe verificar una ecuación que involucra derivadas de la función desconocida. Dichas ecuaciones se denominan ecuaciones diferenciales. Tal vez el ejemplo más conocido es la ley de Newton:

${\displaystyle m{\frac {\mathrm {d} ^{2}u(t)}{\mathrm {d} t^{2}}}=F\left(t,u(t),{\frac {\mathrm {d} u(t)}{\mathrm {d} t}}\right)}$

Isaac Newton se daba cuenta de la importancia que tenían las ecuaciones diferenciales para el análisis de los fenómenos de la naturaleza. En sus renombrados "Principios matemáticos de la filosofía natural" (1687) que engloban mecánica newtoniana, empiezan con la ecuación diferencial del movimiento. Esta ecuación se considera como axioma, mientras que los planteamientos posteriores de la mecánica son, de hecho, teoremas que se derivan de dicho axioma, así como de la ley de gravitación universal que se desgaja de los hechos experimentales (leyes de Kepler) y del mencionado axioma:

Una ecuación diferencial ordinaria (EDO) puede plantearse, siendo F una relación o función, como

(1a)${\displaystyle \ F(x,y,y',y'',\dots ,y^{(n)})=0}$

...para representar la EDO en que la función incógnita (también conocida como variable dependiente), lo es de una única variable independiente.

En general, una ecuación diferencial lineal de orden n puede formularse, siendo cada una función dependiente de t, como:

(1b)${\displaystyle \ a_{n}(t)y^{(n)}+a_{n-1}(t)y^{(n-1)}+\ldots +a_{1}(t)y'+a_{0}(t)y=g(t)}$

Una solución de la ecuación (1a) o (1b) será una "familia" de curvas o funciones del tipo ${\displaystyle y=f(t)\,}$ 
que substituida dentro de la ecuación la convierte en una igualdad en la que todos los términos son conocidos.
En la formulación más simple, la función incógnita es una función para cierto valor real o complejo pero con mayor generalidad, puede serlo para el valor de un vector o matriz, lo que lleva a considerar un sistema de ecuaciones diferenciales ordinarias (EDO) para una única función.

EJEMPLOS

1)

2)

• Método de Euler

En matemática y computación, el método de Euler, llamado así en honor de Leonhard Euler, es un procedimiento de integración numérica para resolver ecuaciones diferenciales ordinarias a partir de un valor inicial dado.

El método de Euler es el más simple de los métodos numéricos resolver un problema del siguiente tipo:

Consiste en multiplicar los intervalos que va de  a  en  subintervalos de ancho 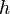; osea:

de manera que se obtiene un conjunto discreto de  puntos:  del intervalo de interes . Para cualquiera de estos puntos se cumlple que:

 .

La condición inicial , representa el punto  por donde pasa la curva solución de la ecuación de el planteamiento inicial, la cual se denotará como .

Ya teniendo el punto  se puede evaluar la primera derivada de 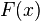 en ese punto; por lo tanto:

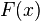Con esta información se traza una recta, aquella que pasa por  y de pendiente . Esta recta aproxima  en una vecindad de . Tómese la recta como reemplazo de  y localícese en ella (la recta) el valor de y correspondiente a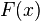 . Entonces, podemos deducir según la Gráfica A:

Se resuelve para :

Es evidente que la ordenada  calculada de esta manera no es igual a , pues existe un pequeño error. Sin embargo, el valor  sirve para que se aproxime  en el punto  y repetir el procedimiento anterior a fin de generar la sucesión de aproximaciones siguiente:

• Método de Taylor 

• Métodos de Runge-Kutta

5 Conclusión

Finalmente y para concluir se determino que, la resolución de problemas de ingeniería está asociada, por lo general, a resultados numéricos puesto que se requieren respuestas prácticas.
La mayor parte de las leyes científicas de expresan en términos de rapidez de variación de una variable con respecto otra.
Además proporcionan una herramienta esencial para modelar muchos problemas en Ingeniería, Física, Economía y Biología, puesto que estos, por lo general, requieren la determinación de una función que satisface a una ecuación diferencial.
El Método de Runge Kutta es mejor que el método de Euler, pero aún así es posible aumentar la precisión achicando los pasos entre los puntos o implementando el método de orden superior.
Es el método más utilizado para resolver numéricamente problemas de ecuaciones diferenciales ordinarias con condiciones iniciales es el método de Runge-Kutte, el cual proporciona un pequeño margen de error con respecto a la solución real del problema y es fácilmente programable en un software para realizar iteraciones necesarias.
El dominio de los métodos numéricos, en combinación con las capacidades y potencialidades de la programación de computadoras resuelve problemas de ingeniería de manera más fácil y eficientemente.

Bibliográfia.

http://www.dma.uvigo.es/~aurea/TR_C2_EDO.pdf

https://sites.google.com/site/metodosnumericosmecanica/home/unidad-vi/62-mtodos-de-un-paso-mtodo-de-euler-mtodo-de-euler-mejorado-y-mtodo-de-runge-kutta

http://campus.usal.es/~mpg/Personales/PersonalMAGL/Docencia/MetNumTema4Teo(09-10).pdf